After giving lectures at the University of California, Berkeley, I uploaded some notes to arxiv and HAL.

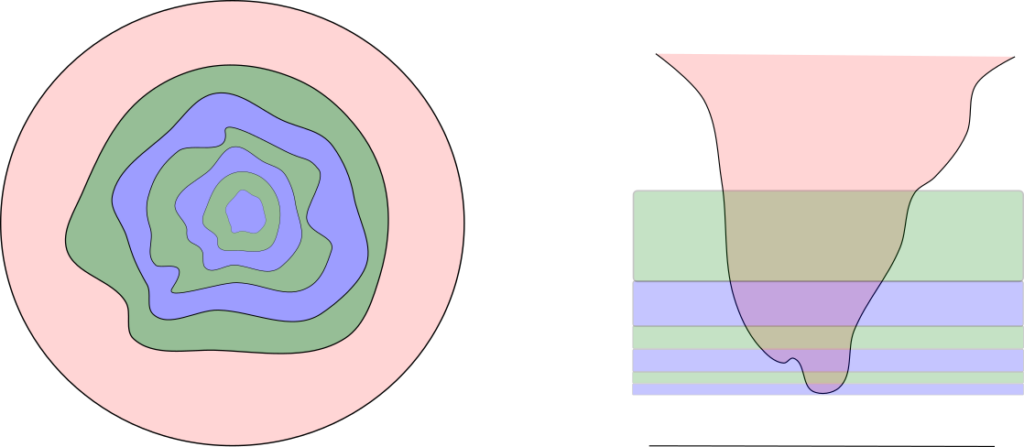
The picture illustrates the iterative procedure in the intermediate value principle (De Giorgi's second lemma).

Abstract. This book presents a comprehensive regularity theory for solutions of elliptic, parabolic, and kinetic equations. The foundation of this theory was laid by E. De Giorgi's groundbreaking resolution of Hilbert's nineteenth problem in 1956. The innovative tools he developed to tackle this problem proved to be remarkably versatile. In 1957, just one year later, J. Nash independently developed analogous techniques for parabolic equations, concurrently with De Giorgi's research. By the year 2000, these techniques had been extended to address elliptic and parabolic equations featuring integral diffusion, such as the fractional Laplacian. More recently, the theory has evolved to encompass kinetic equations, accommodating both local and integral diffusions. This book aims to present these results in a unified and coherent manner, beginning with the classical elliptic framework and progressing through to the most recent advancements in kinetic equations.

Comment. This first version does not contain results for integral diffusions. I hope I will include them in a second version