Cyril IMBERT

De Giorgi’s regularity for elliptic, parabolic and kinetic equations

After giving lectures at the University of California, Berkeley, I uploaded some notes to arxiv and HAL.

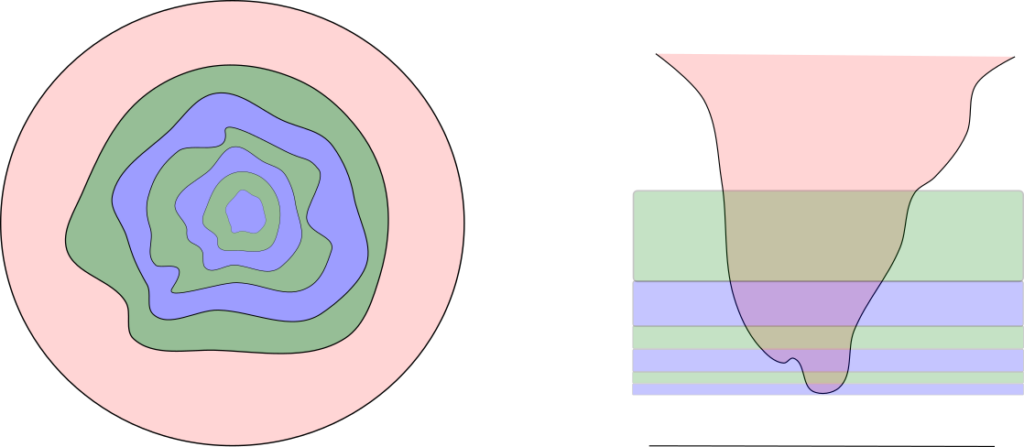
The picture illustrates the iterative procedure in the intermediate value principle (De Giorgi’s second lemma).

Abstract. This book presents a comprehensive regularity theory for solutions of elliptic, parabolic, and kinetic equations. The foundation of this theory was laid by E. De Giorgi’s groundbreaking resolution of Hilbert’s nineteenth problem in 1956. The innovative tools he developed to tackle this problem proved to be remarkably versatile. In 1957, just one year later, J. Nash independently developed analogous techniques for parabolic equations, concurrently with De Giorgi’s research. By the year 2000, these techniques had been extended to address elliptic and parabolic equations featuring integral diffusion, such as the fractional Laplacian. More recently, the theory has evolved to encompass kinetic equations, accommodating both local and integral diffusions. This book aims to present these results in a unified and coherent manner, beginning with the classical elliptic framework and progressing through to the most recent advancements in kinetic equations.

Comment. This first version does not contain results for integral diffusions. I hope I will include them in a second version

Kinetic program in Berkeley

I am one of the organizers of the semester-long program Kinetic Theory: Novel Statistical, Stochastic and Analytical Methods at SLmath in Berkeley.

Overview.

The focus of the proposed program is on so-called kinetic equations, describing the evolution of the of many-particle interacting systems. These models have the form of statistical flows, with their solutions being either a single or multiple point probability density functions or measures, supported in a space of attributes. The attributes are problem-dependent and can be molecular velocity, energy, opinion, wealth, and many others. The flow then predicts the evolution of the probability measure in time, position in space, and the interchanging of the particles’ states by the transition probability.

Probably the most classical kinetic equation is the Boltzmann equation which describes the evolutions of the phase-space density function for a dilute gas under binary molecular collisions. Other well-known classical kinetic models include the Landau equation, Vlasov equation for plasmas or other systems, Fokker-Planck equations or kinetic formulations of various macroscopic or hyperbolic systems.

In recent years, the successes of kinetic theory gave rise to an rapidly increasing variety of mathematical models beyond physics to applications in life sciences, social sciences, economy. Even more recently fascinating connections between kinetic theory and some aspects of data science have emerged.

Kinetic theory has strong and fascinating interactions with a large variety of other fields, including statistical mechanics, stochastic processes, dynamical systems…

The program will strive to give an overview of the novel mathematical tools used in kinetic theory through a broad range of classical and more recent applications.